Как вычислить корень из большого числа без калькулятора

Во многих ситуациях необходимо вычислить корень из числа без калькулятора, например, на экзамене. Вам может показаться это довольно сложной задачей, которая занимает уйму времени, особенно если дано дробное или крупное число.

В этой статье мы опровергнем этот миф и покажем, как быстро вычислить корень из числа в уме несколькими способами.

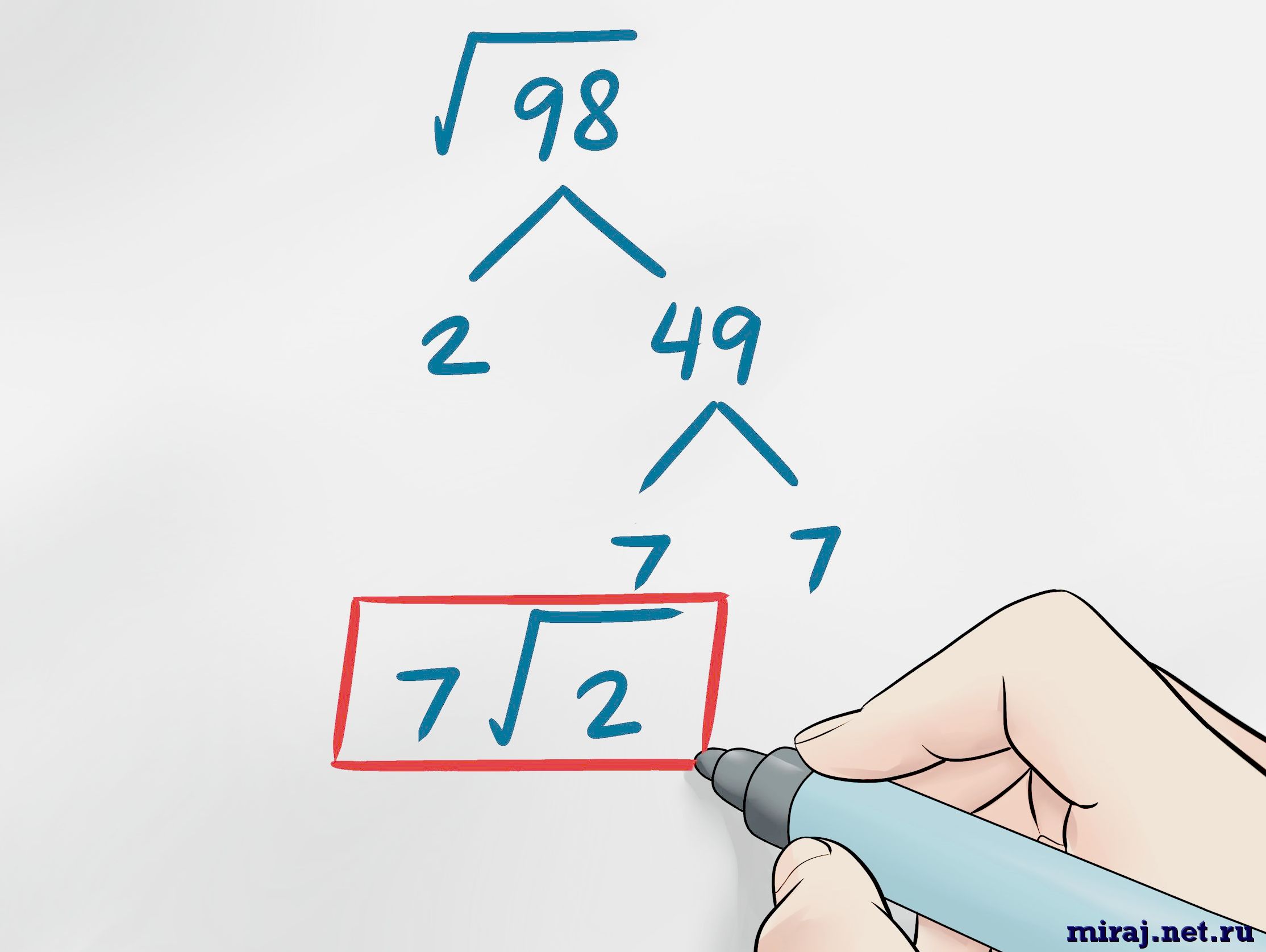
Способ разложения на множители.

Для этого способа необходимо выучить несколько признаков делимости:

• На 2 делятся четные числа
• На 3 делятся числа, сумма цифр в которых поделится на 3, например, 123. Здесь к 1 прибавляем 2 и 3, получив 6. Это число делится на 3.
• На 4 делятся числа последние две цифры которых являются нулями, например, 100. А также число, последние две цифры которого являются двузначным числом, делимым на 4, например, 216.

Исходя из признаков делимости, выбираем цифру на которую будет делиться число 12 816. В нашем случае это 4. Далее просто делим 12 816 на 4 в столбик. Получаем 324. Его можно разделить либо 3, либо на 4. Весомой разницы нет. Мы разделим на 4, потому что так быстрее. Получаем 81 и из таблицы умножения знаем, что 81 = 9².

Выписываем все делители под знак корня и делаем их квадратными (4*4 = 4²; 81 = 9²).

Корень числа, как известно, равен данному числу в квадрате, поэтому выносим 4 и 9 из-под корня без квадрата. Далее просто перемножаем эти числа и получаем ответ. В нашем случае – это 36.

Данный способ хоть и простой, но может не подойти ко всем числам, ведь некоторые из них делятся только на двузначные или трехзначные числа.

Способ, который подойдет для любого числа с целым корнем

Этот способ сложнее, но благодаря ему можно вычислить корень из большого числа.

Для него нужно знать квадраты чисел от 1 до 9. Нам понадобится только последняя цифра квадрата. Например, квадрат 6 – 36. Запишем только шестерку. И так с каждой цифрой.

Для нахождения корня, мы воспользуемся формулой: (десятки + единицы) ²= десятки² + 2*десятки*единицы + единицы²

Суть метода тяжело раскрыть на словах, поэтому продемонстрируем на примере.

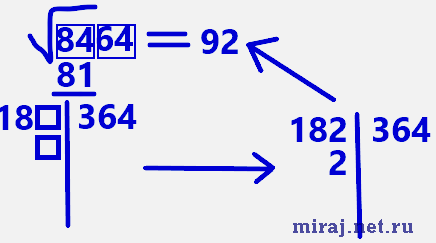
Допустим, нам необходимо вычислить корень из числа 8 464. Сначала мы разбиваем число на группы двузначных чисел справа налево.

Находим цифру, квадрат которой является минимальным приближенным к двузначному числу слева. Здесь это 9. Записываем цифру в результат и вычитаем из 84 квадрат девятки. То есть 84-81.

Получаем цифру три и располагаем ее справа от столбца. Туда же выписываем двузначное число, которое расположено правее – 64. Слева от столбца пишем девятку, умноженную на два, оставив две клеточки, как показано на картинке.

Далее в эти две клеточки выписываем цифру, с помощью которой, образуется трехзначное число, умножив которое на вписанную цифру, должно получиться такое же число, что и справа от столбца или наименьшее приближенное к нему.

Цифру, которой мы воспользовались (в этом случае – 2) выписываем в результат после девятки и получаем решение.

Если число пятизначное, шестизначное или более, нужно проделать процедуру из последних, указанную в последних трех абзацах, еще один раз. Продемонстрирую это на втором примере.

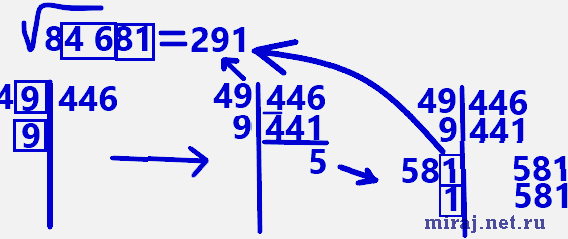
Возьмем пятизначное число 84 681 и разделим его на блоки двузначных чисел справа налево. В числе с пятью знаками слева остается одна цифра, и это нормально. Находим цифру, квадрат которой является минимальным приближенным числом к восьми. Это 2. Пишем ее после знака равно.

Из восьми вычитаем квадрат двойки – четверку. Выписываем разницу справа от столбика, а слева пишем двойку, умноженную на 2.

Сносим второй блок, который расположен правее и получаем число 446 справа от столбца.

Находим такую цифру, приписав которую к четверке и умножив полученное двузначное число на нее же, получится минимальное число приближенное к 446. Это девятка. Запишем ее в результат после двойки.

49 умножим на 9 и получим 441. Запишем его справа от столбца, под 446.

Вычтем из 446 число 441. Запишем разницу и снесем следующее двузначное число – 81. Получим 581.

Слева от столбика напишем произведение 29 (число после знака равно) и двойки. Далее воспользуемся табличкой, которую составили ранее: трехзначное число справа оканчивается единицей. Квадрат цифры 1 и 9 тоже ею оканчивается. Применив логическое мышление, можно понять, что число слева от столбца должно оканчиваться единицей. Следовательно, получаем число 581 и умножаем его на 1.

Числа справа и слева от столбца сходятся, значит все решено правильно. Припишем единицу к 29 в ответе и получим 291. Это число и является решением.

Стоит понимать, что способ не сработает если корнем окажется число с остатком!

Способ для вычисления корней с остатком

В большинстве случаев корень является числом с остатком. Этот метод поможет найти такой корень.

Он работает по принципу разложения числа на множители. Покажем на примере.

Допустим, нужно найти корень из 45. Раскладываем это число на множители (можно воспользоваться способом из начала статьи или сделать это самостоятельно). 45 = 5*9. Девять является квадратом трех, следовательно нужно вынести 3 из-под знака корня. Пятерка же не является квадратом какого-либо числа, поэтому она остается под корнем.

Ту же операцию можно проделать и с числом 320, которое можно разделить на множители 64 и 5. 64 – квадрат восьми, поэтому последнее выносится из-под корня, а 5 остается под ним.

Способ оценки

Способ подойдет для быстрого вычисления корня из четырехзначного числа. Чтобы его применить, нужно знать или иметь доступ к таблице квадратов из второго способа.

Выбираем самое маленькое приближенное к 6084 двузначное круглое число и, полагаясь на однозначные числа, возводим его в квадрат. Так же поступаем и с наибольшим числом, приближенным к 6084.

Таким образом, мы получаем диапазон чисел, между которыми нужно искать ответ.

Узнать вторую цифру можно воспользовавшись таблицей представленной выше.

Просмотрев ее, становится понятно, что это либо 2 либо 8.

Воспользовавшись цифрой 2, получим число 72. 72 в квадрате = 5184. Поэтому такой ответ нам не подходит остается цифра восемь.

Получаем ответ 78.