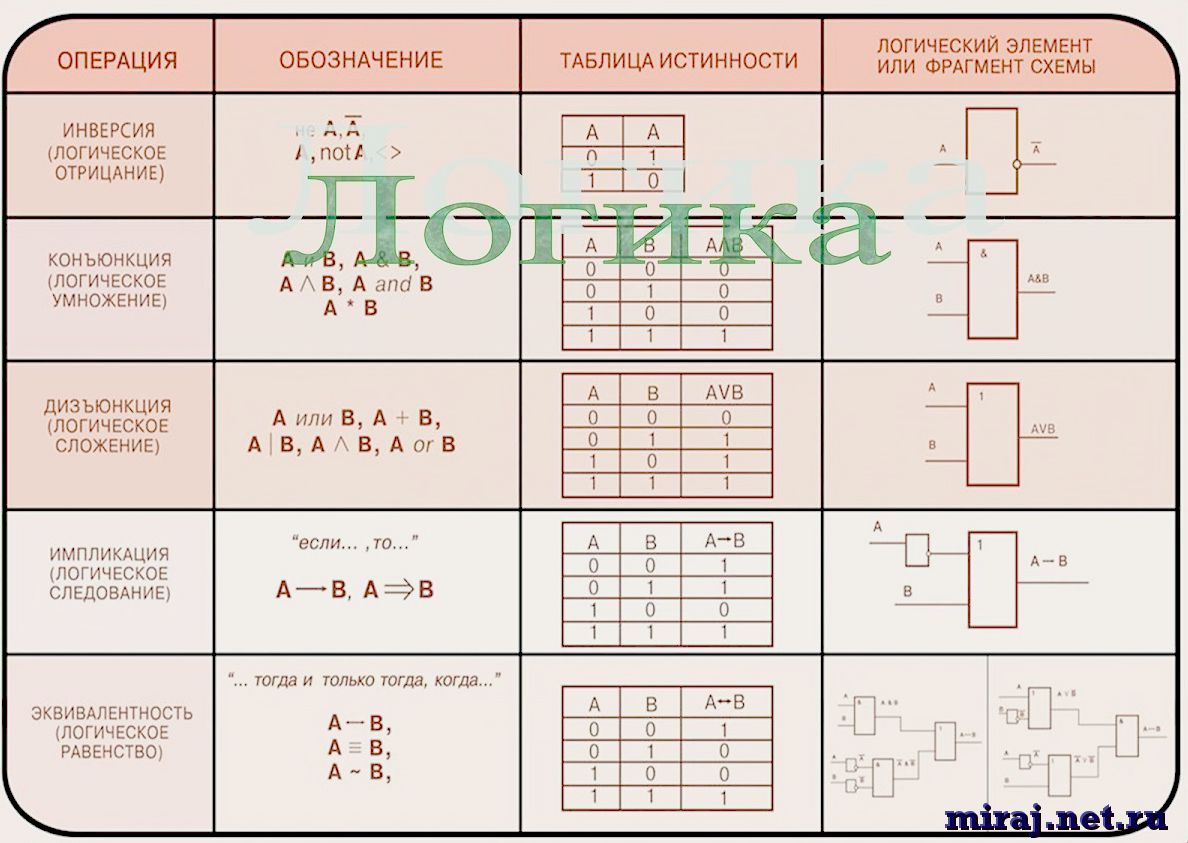
Система в полном исполнении называется базисом. Минимальные возможности представлены в виде функций. Булев базис – это структура, состоящая из набора элементарных действий. Это функции, которые будут описаны ниже. Полностью информировано пространство, в котором применяются все свойства. Каждая система имеет свою структуру и состав.
Система характеристик
Базис булевых функций – полная система характеристик и признаков. Без нарушений и изъянов существуют выражения. Не исключается ни единая функция. Распространенный базис представляет собой полную систему. В ней содержатся элементарные функции. Местоимения И, ИЛИ И НЕ – это основные операции. Логические действия предусмотрены законами математики.
Логическая схема
Необходимо построить в булевом базисе логическую схему, которая будет завершающим этапом явления. Она описывает законы. Приводятся примеры базиса множества булевых функций.
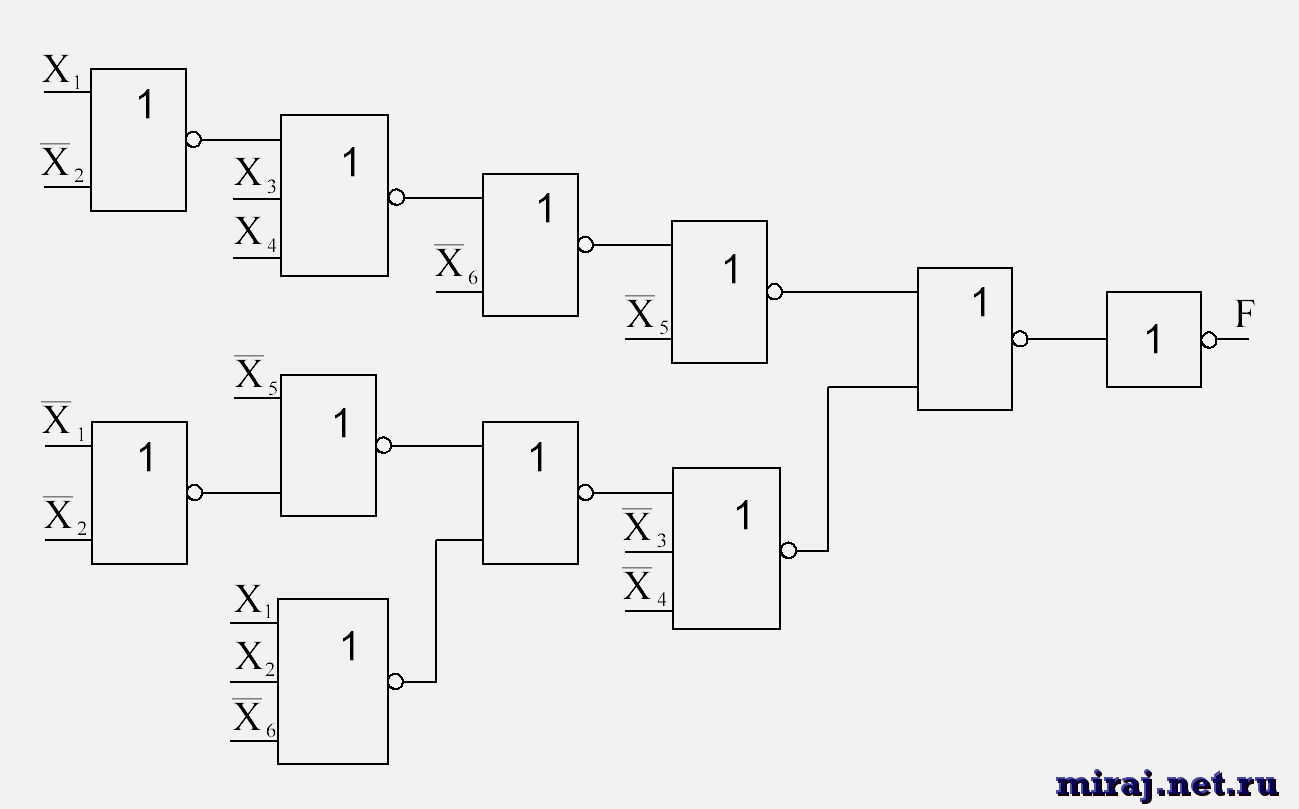
Существует сочетательный закон. Это ассоциативное понятие, которое применятся в математике. Правила гласят, что итоговый исход будет результатом последовательного выполнения действий. Это одноименные операции логистических данных. Не происходит зависимости от х1(х2х3) = (х1х2)х3; х1 + (х2 + х3) = (х1 + х2) + х3.
Базисы в булевой алгебре применяются часто. Алгебраические операции становятся примером правильных решений. Предусмотрен базис полной системы булевых функций. Это две элементарные функции. Они относятся к основному положению.
Законы булевых функций
Распределительный закон подразумевает под собой дистрибутив. Здесь операции выполняются последовательно с логическим пониманием цепи. Местами меняются значения. Пример х1 (х2 + х3) = х1х2 + х1х3, х1 + х2 х3 = (х1 + х2) (х1 + х3).
Есть другой коммутативный закон, который позволяет перемещать значения. Исходные данные не зависит от изменения мест множителей. Слагаемые будут измены.
х1 х2 = х2 х1; х1 + х2 = х2 + х1.
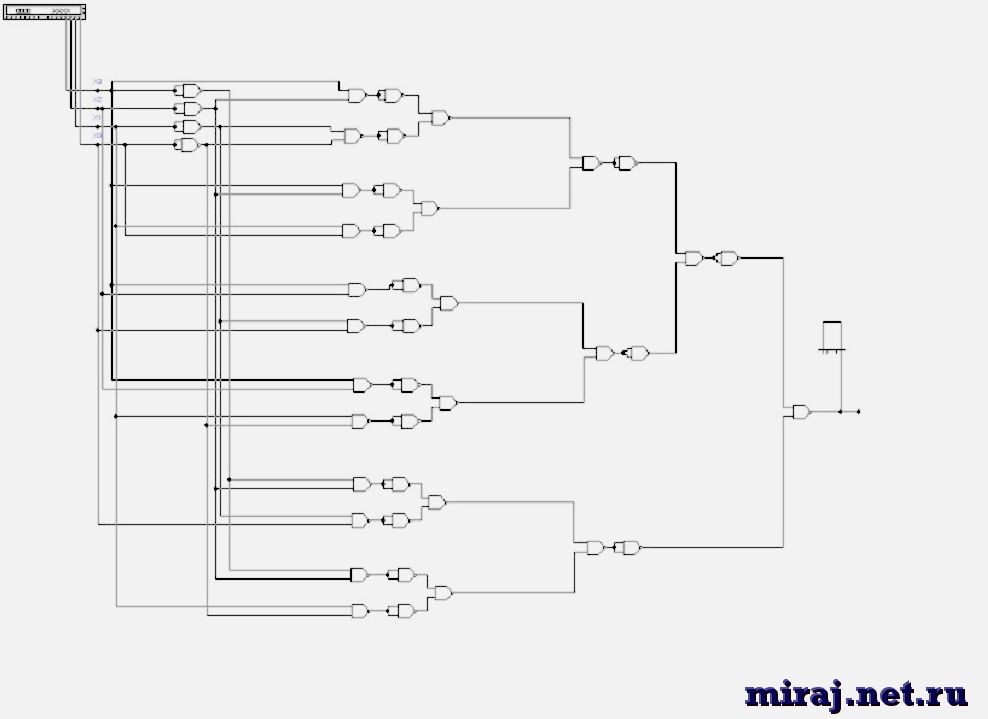
Следующим законом является – двойственность. По понятиям де Моргана. Здесь происходит инверсия дизъюнкции. Так, логические операции при сложении становятся эквивалентны конъюнкции. Это умножение.
Правило диктует свои значения, которые являются примером для учеников. Они используют данные варианты. Согласно законам действует положение, при котором исходная ФАЛ (f(x1, x2) = x1 + x2) будет равна двойственному значению. Базис системы булевых функций представлен переменными.