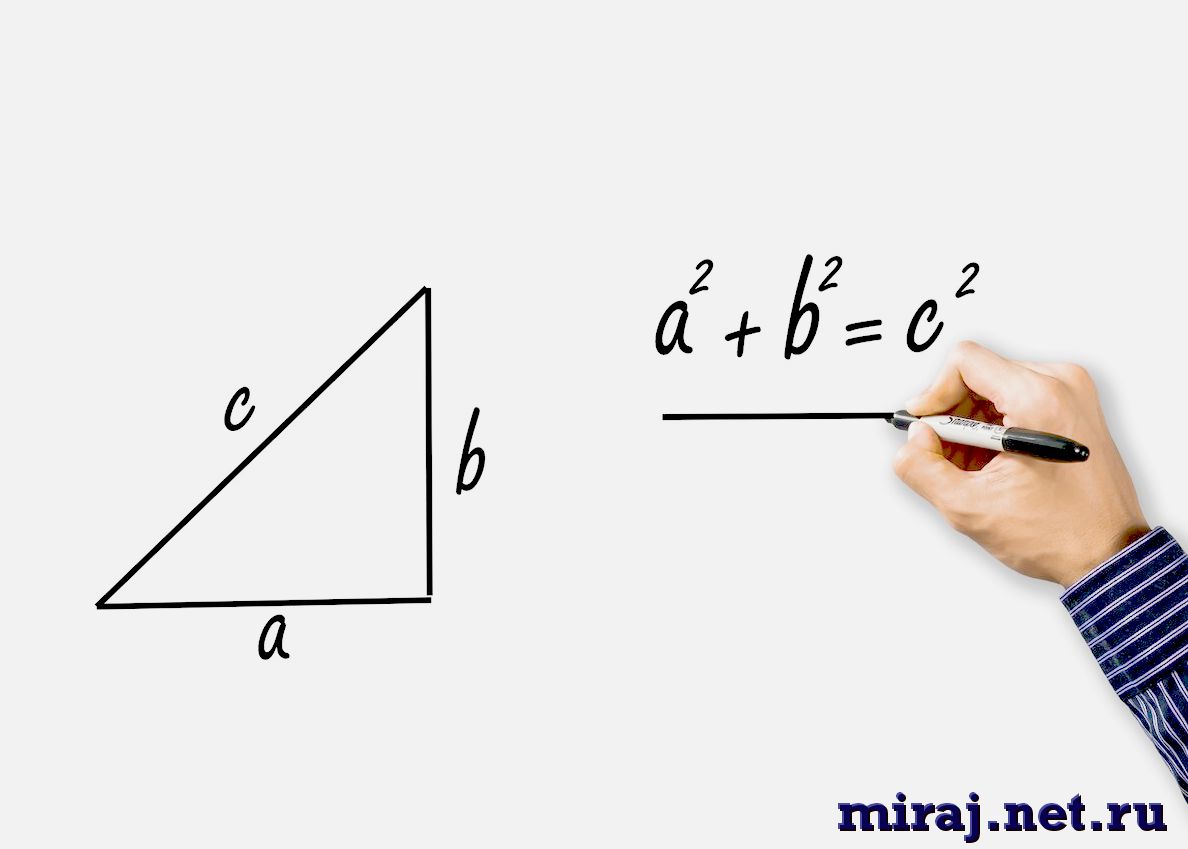В науке существует более трёхсот доказательств теоремы Пифагора. В школьном курсе затрагиваются самые простые доказательства, которые выводятся из главных формулировок.
Главное значение теоремы Пифагора, которое наизусть заучивал каждый школьник, звучит так: квадрат гипотенузы равен сумме квадратов катетов.
Речь идёт о длине сторон в треугольнике, где один из углов = 90 градусов, гипотенуза – находится напротив него, а катеты образуют его.
Теорема может записываться с помощью буквенных обозначений:
А² + В² = С², где А и В – катеты, а С – гипотенуза
Из неё можно вывести следующие равенства:
А = √С²– В²
В = √С² – А²
С = √А² + В²
То есть в любом треугольнике, имеющем прямой угол, сумма длины катетов будет равняться квадратной длине гипотенузы.
Доказательство Прямой теоремы Пифагора
Если в задании сказано: докажите теорему Пифагора кратко, то удобнее всего будет сделать это следующим способом:
Дано: прямоугольный треугольник МND, угол D=90 градусов.
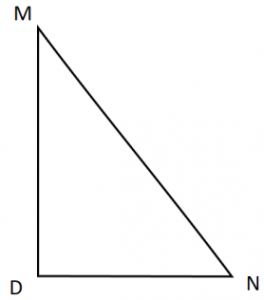
Доказать: теорему Пифагора, т.е. MN² = MD² + DN².
Ход работы:
Проведем отрезок из вершины D на гипотенузу MN, точку пересечения обозначим буквой Н, так, чтобы угол DНN получился равным 90 градусов, то есть прямым. При этом DH будет являться высотой.
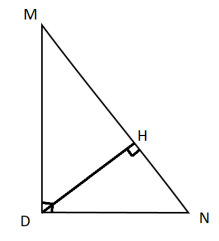
Треугольники MDN и MDН являются подобными по двум углам, так как угол MDN = DНN = 90 градусов, а угол DMH является общим.
Треугольники DНN и MDN так же подобны по двум углам: DНN = MDN = 90 градусов, а угол DNH является общим для двух треугольников.
Для удобства введем новые короткие обозначения сторон: MN = d, ND = m, MN = n.
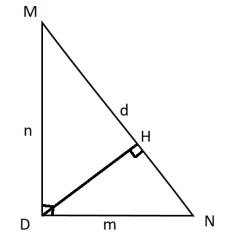
Из подобия треугольных фигур, доказанного выше, получим следующие равенства:
- Отношение m и d = отношению NH и m;
- Отношение n и d = отношению MH и n.
Из полученных равенств выведем формулы: m² = d * NH; n² = d * MH, а затем сложим их друг с другом:
m² + n² = d * NH + d * MH;
m² + n² = d (NH + MH).
По рисунку сумма длин NH и MH равно стороне MN, заменим их в готовой формуле:
m² + n² = d * MN
А сторона MN является стороной d, которую мы назвали так для удобства обозначения.
Итак, приведём формулу к виду:
m ²+ n² = d²
А теперь заменим введенные нами буквенные обозначения на изначальные:
MN² = MD² + DN², что и требовалось доказать.
Это был один из самых легких способов доказать теорему Пифагора, поскольку здесь использовалось так называемое прямое утверждение.
Обратная теорема
Существуют задания, в которых просят сформулировать и доказать обратную теорему Пифагора.
Она звучит так:
Если при сложении квадратов каждой стороны фигуры получилось число, равное квадрату 3-й стороны, то эта фигура – треугольник с прямым углом. Иными словами, если длины сторон, образующих прямой угол, умножить сами на себя и полученные произведения сложить, должен получиться квадрат стороны, лежащей против угла в 90 градусов.
Доказательство обратной теоремы Пифагора
Дано: фигура MDN
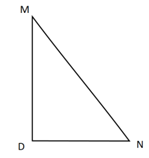
Доказать: MDN – прямоугольный треугольник, то есть угол D = 90 градусов.
Доказательство:
нарисуем прямой угол с вершиной D ₁. При этом на его сторонах построим отрезки D ₁M ₁ равный DM и D₁N ₁, равный DN;
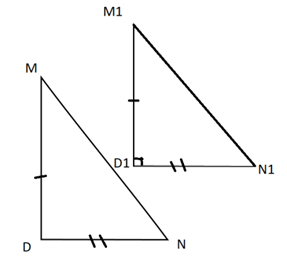
Проведем отрезок M ₁N ₁. В результате получится прямоугольный треугольник M ₁D ₁N ₁, где угол D ₁ = 90 градусов.
В полученной фигуре пробуем применить теорему Пифагора:
M ₁N ₁² = M ₁D ₁² + D ₁N ₁² ;
MN² = MD² + DN²;
M ₁D ₁ = MD; DN = DN, из чего следует, что приведенные выше равенства равны между собой, то есть MN = M ₁N ₁.
Значит: D ₁N ₁ = DN – по построению, M ₁D ₁ = MD – по построению, MN = M ₁N ₁ по доказанному результату.
Треугольники MDN и M ₁D ₁N₁ равны по трём сторонам.
Соответственно, угол D = углу D₁ = 90 градусов, то есть треугольник MDN – прямоугольный, что и требовалось доказать.
Неважно, сколько способов доказать Теорему Пифагора существует в науке, в школьной программе обычно проходят только два из них.