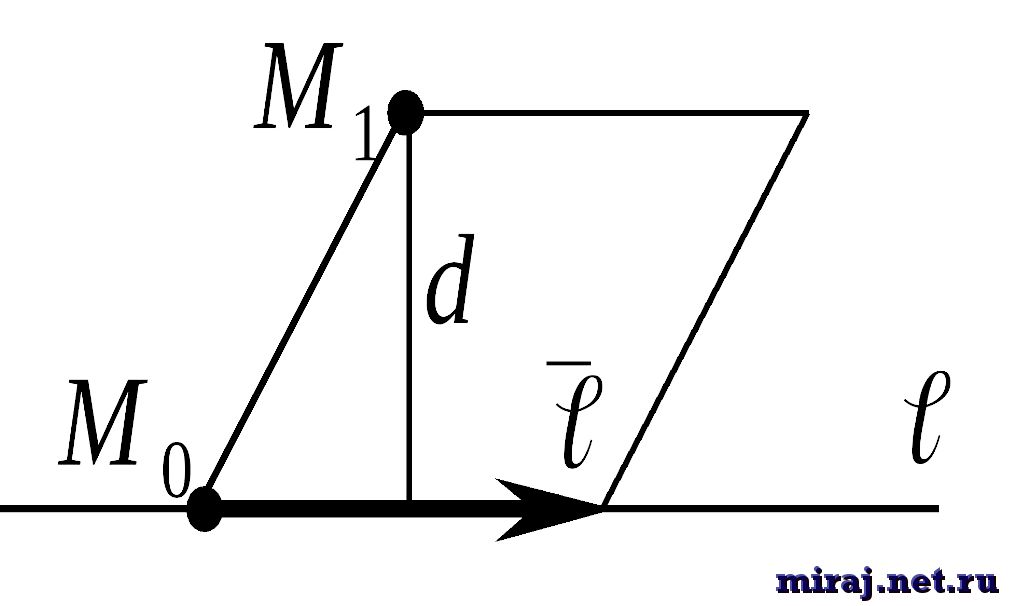
Здесь вы узнаете: что такое отклонение точки от прямой и как его найти.
Что такое отклонение точки от прямой?
Отклонение точки на плоскости – это расстояние от точки до прямой.
Если точка лежит в противоположном направлении от координаты (0;0) относительно прямой, то расстояние будет равно результату со знаком плюс; в случае если она лежит там же, где и начало координат, расстояние будет иметь знак минус.
Иногда могут возникнуть альтернативные случаи:
- Прямая пересекается с началом координат. В таком случае отклонение равно самому расстоянию и будет идти с плюсом.
- Точка находится в той стороне, которая будет сонаправлена вектору. Здесь полученный результат будет со знаком минус, и так же будет равен самому расстоянию.
Теорема: отклонение точки от прямой на плоскости
Пусть данная прямая определяется по нормальному уравнению. Тогда отклонение на плоскости эквивалентно нормальному уравнению.
Отклонение точки от прямой формула
Определить отклонение означает найти расстояние. Чтобы это сделать используется нормальное уравнение прямой: «хcosA+уsinA+R=0».
В этом уравнении, угол A – угол между осью абсцисс и вектором заданной прямой B; R – промежуток между началом координат до B.
При нахождении отклонения, в уравнение вместо x и y нужно подставить данные нам координаты. Ниже мы рассмотрим несколько примеров для решения.
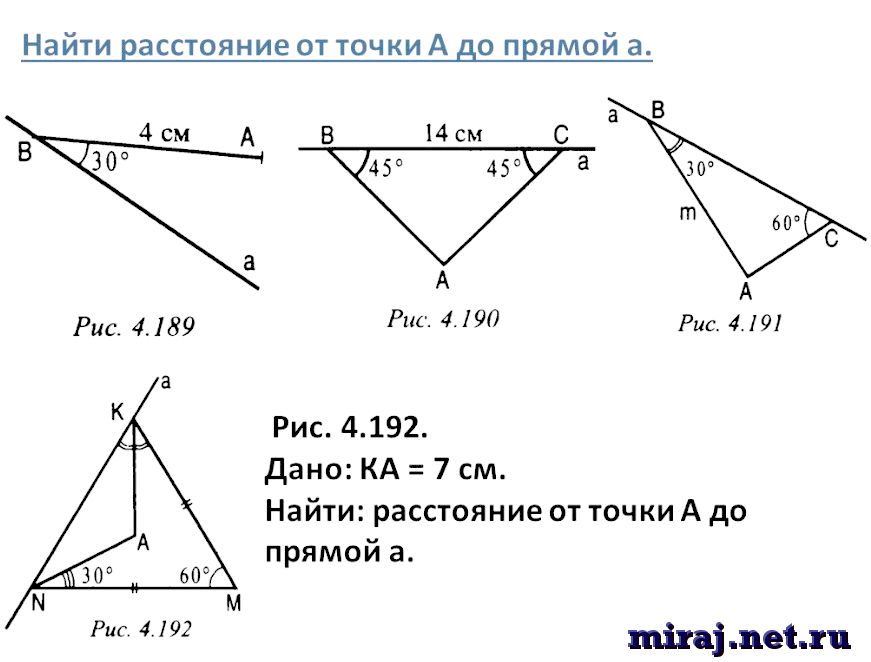
Как найти отклонение точки от прямой?
Задача 1
Дано: 7/9x+5y+8.9=0
Найдите: отклонение A (-5;6).
Для решения мы подставляем в уравнение заданные координаты. Тогда получается следующее:
7/9*(-5)+5*6+8.9=41.9
Задача 2
Дано: 9х-23у-1=0
Найдите: отклонение А (3;12)
Решение: 9*3-23*12-1=-250
Внимание! Если вам дан рисунок, не забывайте обращать внимание на то, в какой области лежит точка – это влияет на знак полученного результата.
Как найти отклонение через нормирующий множитель?
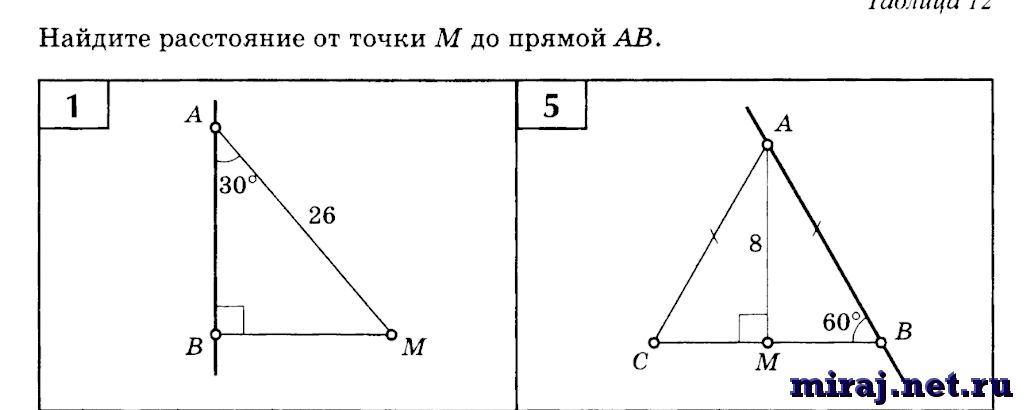
Еще один способ нахождения отклонения – привидение заданной прямой к нормальному виду. Чтобы это сделать, каждый член заданного уравнения нужно перемножить на нормирующий множитель – он обозначается буквой t и равен 1/5. Для определения его знака мы смотрим на знак последнего члена уравнения r – если у него стоит знак плюс, то у t будет минус, и наоборот. То есть у нормирующего множителя должен стоять знак, противоположный знаку третьего члена уравнения.
Рассмотрим пример с привидением прямой к нормальному виду:
Задача 1
5х-6у+7=0
Знак последнего члена положительный, значит все члены умножаем -1/5.
У нас получается уравнение -1х+6/5у-7/5=0
После привидения уравнения к нужному виду, мы можем подставить значения точки и высчитать получившееся значение.
Задача 2
Дано: х-2у-9=0
Найдите: отклонение А (8;-1)
Решение: х/5-2у/5-9/5=8/5+2/5-9/5=0.2
Важно! Второй способ используется в случаях, когда в условии указано общее уравнение прямой. Если в условии уже дано нормальное уравнение, нужно просто подставить значения координат и получить результат.